
- Avtor Lynn Donovan [email protected].
- Public 2023-12-15 23:53.
- Nazadnje spremenjeno 2025-01-22 17:40.
Razvrsti z združitvijo : uporablja v scenarijih baze podatkov, ker je stabilen (več ključev razvrsti ) in zunanji (rezultati se ne prilegajo pomnilniku). Uporabno v porazdeljenih scenarijih, kjer med ali po njem prispejo dodatni podatki razvrščanje . Poraba pomnilnika preprečuje širšo uporabo na majhnih napravah, vendar obstaja različica Nlog^2N na mestu.
Če upoštevamo to, kje se uporablja razvrščanje z vstavljanjem?
Uporablja: Razvrščanje vstavljanja je uporablja ko je število elementov majhno. Uporabno je lahko tudi, ko je vhodni niz skoraj razvrščeno , le nekaj elementov je napačno postavljenih v popolno veliko polje. Kaj je binarno Razvrščanje vstavljanja ? Binarno iskanje lahko uporabimo za zmanjšanje števila primerjav v običajnem vstavljanje razvrščanja.
Veš tudi, kaj je razvrščanje z združitvijo s primerom? An primer od razvrščanje z združitvijo . Najprej razdelite seznam na najmanjšo enoto (1 element), nato pa primerjajte vsak element s sosednjim seznamom razvrsti in združiti dva sosednja seznama. Končno so vsi elementi razvrščeno in združeni . Združi razvrščanje je algoritem deli in vladaj, ki ga je izumil John von Neumann leta 1945.
Zakaj se v zvezi s tem uporablja razvrščanje spajanja?
Razvrsti z združitvijo je uporaben za razvrščanje povezane sezname. Razvrsti z združitvijo je stabilna razvrsti kar pomeni, da isti element v nizu ohranja svoje prvotne položaje drug glede na drugega. Celotna časovna zapletenost Združi razvrščanje je O(nLogn). Učinkovitejši je, saj je v najslabšem primeru tudi čas izvajanja O(nlogn)
Kako uporabljate razvrščanje z združitvijo?
Tukaj je opisano, kako razvrščanje z združevanjem uporablja deli in vladaj:
- Razdelite tako, da poiščete število q položaja na sredini med p in r.
- Osvojite z rekurzivnim razvrščanjem podnizov v vsakem od dveh podproblemov, ustvarjenih s korakom delitve.
- Združite tako, da združite dve razvrščeni podnizi nazaj v en sam razvrščeni niz [str.
Priporočena:
Kje se uporabljajo algoritmi za razvrščanje?

Kratek pregled aplikacij za razvrščanje. Komercialno računalništvo. Poiščite informacije. Raziskave operacij. Simulacija na podlagi dogodkov. Numerični izračuni. Kombinatorno iskanje. Primov algoritem in Dijkstrin algoritem sta klasična algoritma, ki obdelujeta grafe
Kako se izračuna kompleksnost razvrščanja z združitvijo?
2 odgovora. Razcepitev vozlišča A[L,R] na dve vozlišči traja R−L+1 čas, nato pa združitev dveh podrejenih vozlišč A[L,M] in A[M+1,R] ponovno zahteva A[R−L +1] čas. Tako je za vsako vozlišče število operacij, ki jih izvede algoritem, enako dvakratni velikosti matrike, ki ustreza temu vozlišču
Kakšna je razlika med združitvijo in združitvijo v SQL?
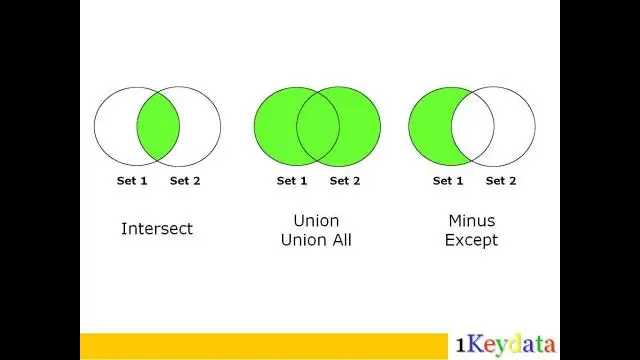
V sindikatu se stolpci ne združijo za ustvarjanje rezultatov, vrstice so združene. Za združevanje podatkov iz ene ali več tabel v en sam rezultat je mogoče uporabiti tako združitve kot združitve. Oba se tega lotita na različne načine. Medtem ko se spoj uporablja za združevanje stolpcev iz različnih tabel, se združitev uporablja za združevanje vrstic
Kakšna je razlika med združitvijo in IsNull SQL?

Glavna razlika med COALESCE in ISNULL je razlika v ravnanju z različnimi vrstami podatkov. Podatkovni tip izraza COALESCE je podatkovni tip vhoda z najvišjo prednostjo tipa podatkov. Podatkovni tip izraza ISNULL je tip podatkov prvega vhoda
Za kaj se uporablja razvrščanje kopice?
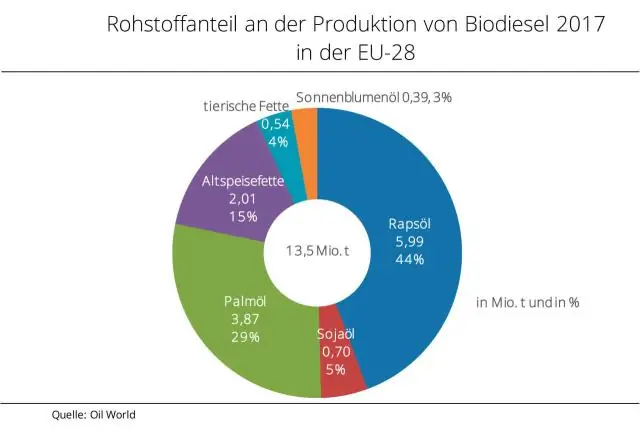
Algoritem razvrščanja kopice se pogosto uporablja zaradi svoje učinkovitosti. Razvrščanje kopice deluje tako, da pretvori seznam elementov, ki jih je treba razvrstiti v podatkovno strukturo kopice, binarno drevo z lastnostmi kopice. V binarnem drevesu ima vsako vozlišče največ dva potomca
