
- Avtor Lynn Donovan [email protected].
- Public 2023-12-15 23:53.
- Nazadnje spremenjeno 2025-01-22 17:40.
Implementacija drevesa binarnega iskanja (BST) v Javi
- Levo poddrevo vozlišča vsebuje samo vozlišča s ključi, manjšimi od ključa vozlišča.
- Desno poddrevo vozlišča vsebuje samo vozlišča s ključi, večjimi od ključa vozlišča.
- Vsako levo in desno poddrevo morata biti tudi a binarno iskalno drevo .
- Ne sme biti podvojenih vozlišč.
Vprašanje je tudi, kako je binarno iskanje implementirano v Javi?
Oglejmo si primer binarnega iskanja v Javi, kjer bomo iskali element iz matrike z uporabo rekurzije
- razred BinarySearchExample1{
- javno statično int binarySearch(int arr, int prvi, int zadnji, int ključ){
- če (zadnji>=prvi){
- int mid = prvi + (zadnji - prvi)/2;
- če (arr[mid] == ključ){
- vrnitev sredi;
- }
Drugič, kje uporabljamo binarno iskalno drevo? Binarno iskalno drevo - Rabljen v veliko Iskanje aplikacije, kjer podatki nenehno vstopajo/odhajajo, kot so zemljevid in nastavljeni objekti v knjižnicah številnih jezikov. Binarno Space Partition - Rabljen v skoraj vsaki 3D video igrici, da določite, katere predmete je treba upodabljati.
Samo tako, kako nastanejo binarna drevesa?
Ustvarjanje binarnega drevesa z uporabo rekurzije
- Preberite podatke v x.
- Dodeli pomnilnik za novo vozlišče in shrani naslov v kazalec p.
- Podatke x shranite v vozlišče p.
- Rekurzivno ustvarite levo poddrevo p in ga naredite za levo poddrevo p.
- Rekurzivno ustvarite desno poddrevo p in ga naredite kot desno poddrevo p.
Kakšna je kompleksnost binarnega iskanja?
Binarno iskanje zažene v najslabšem logaritemskem času, pri čemer naredi O(log n) primerjave, kjer je n število elementov v matriki, O je zapis Big O in log je logaritem. Binarno iskanje zavzema konstanten (O(1)) prostor, kar pomeni, da je prostor, ki ga zavzame algoritem, enak za poljubno število elementov v matriki.
Priporočena:
Kako omogočim iskalno polje v sistemu Windows 10?
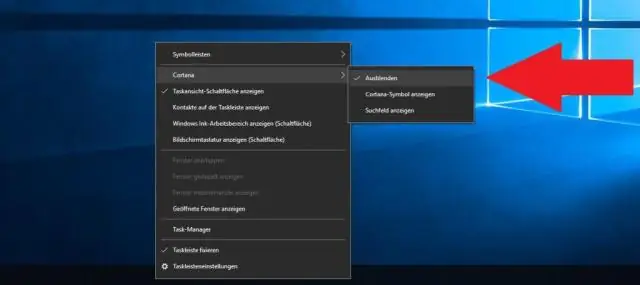
Če je vaša iskalna vrstica skrita in želite, da se prikaže v opravilni vrstici, pritisnite in držite (ali z desno tipko miške) na opravilni vrstici in izberite Iskanje > Pokaži iskalno polje
Kako implementirate GitLab?

Namestitev GitLab Namestite in konfigurirajte potrebne odvisnosti. Dodajte skladišče paketov GitLab in namestite paket. Prebrskajte do imena gostitelja in se prijavite. Nastavite svoje komunikacijske nastavitve. Namestite in konfigurirajte potrebne odvisnosti. Dodajte skladišče paketov GitLab in namestite paket
Kako implementirate nastavljeni vmesnik v Javi?
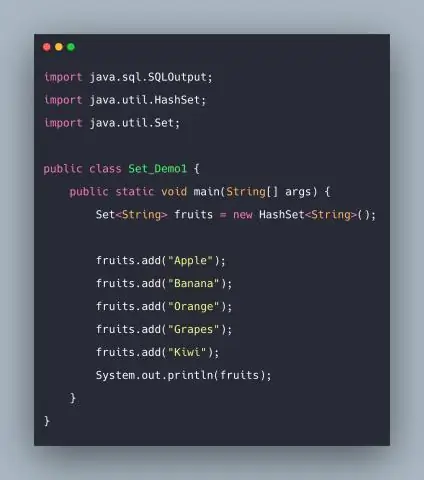
Set v Java Set je vmesnik, ki razširja zbirko. Je neurejena zbirka predmetov, v kateri ni mogoče shraniti podvojenih vrednosti. V bistvu Set izvajajo HashSet, LinkedHashSet ali TreeSet (razvrščena predstavitev). Set ima različne metode za dodajanje, odstranjevanje jasnosti, velikosti itd. za izboljšanje uporabe tega vmesnika
Kako implementirate odločitveno drevo v Pythonu?
Pri izvajanju drevesa odločanja bomo šli skozi naslednji dve fazi: Faza gradnje. Predhodno obdelajte nabor podatkov. Razdelite nabor podatkov iz vlaka in preizkusite s paketom Python sklearn. Usposobite klasifikator. Operativna faza. Naredite napovedi. Izračunaj natančnost
Kako implementirate abstraktni razred v Javi?

Če je razred razglašen za abstrakten, ga ni mogoče ustvariti. Če želite uporabiti abstraktni razred, ga morate podedovati iz drugega razreda, zagotoviti implementacije za abstraktne metode v njem. Če podedujete abstraktni razred, morate zagotoviti implementacije za vse abstraktne metode v njem
